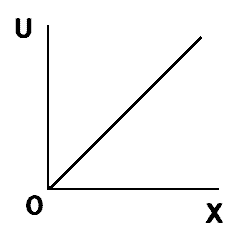「需要曲線」は、消費者の行動を表します。
右下がりの需要曲線
一般的に右下がりの形になります。これは、価格が下がると、需要量が増えることを表しています。
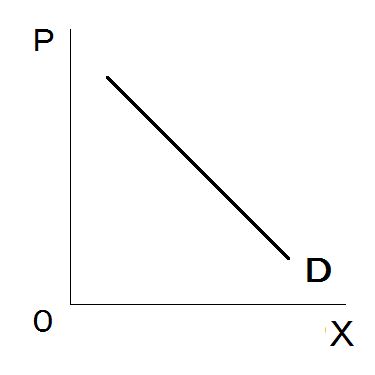
中学の公民では、これのことは当然のこととして学習しましたが、経済学では、「なぜ右下がりになるのか?」について、消費者の行動の理由を考えていきます。
欲望(効用)の世界
経済学が想定する世界では、人々は、自分の欲望に忠実です。消費者は、自分の満足感(効用)を増やすように行動します。この効用は、「効用曲線」で表されます。効用曲線は、「限界効用逓減の法則」により、次のような形が一般的になります。
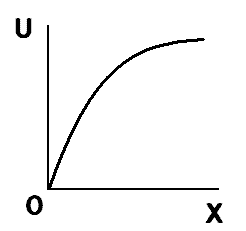
ただ、この効用曲線だけでは、「需要曲線」の内容を説明できません。
なぜか?
モノの値段である「価格」と、お買い物に使えるお金、つまり「予算」について考えていないからです。
ただ、この価格についても、正確に考える必要があります。たとえば、1個100円のパンが、1個200円になったとしましょう。これは、値上げです。でも、パン以外の商品の価格が10倍になったとしたらどうでしょうか?名目的には値上げですが、実質的には値下げになります。
このように、財の価格について考える場合は、他の財の価格と比較する必要があります。このような価格の考え方を「相対価格」(relative price)といいます。ある財について、この「相対価格」を考える場合、(当たり前ですが)別の財についても取り上げる必要があります。
よって、説明のために、「2つの財」について考えることになります。ここから、「無差別曲線」と「予算制約線」の分析につながります。