価格の決まり方を分析するミクロ経済学で、最初の頃に学ぶテーマです。ややこしいので、まずはイメージをつかんでください。
限界効用逓減の法則
うまい!!!

うまい!!

たしかにうまいんだけど、もうひとつ工夫がほしいね。

普段の生活でよくあるケースです。実は、これがミクロ経済学では非常に重要な前提となります。
言葉の意味をみていきましょう。
効用 utility
商品を買うと、満足感が得られます。この満足感を経済学では「効用」utilityといいます。この満足感(効用)は、数値で測れると仮定して、話をすすめていきます。
買った量(消費量)と満足感(効用)の組み合わせを式で表したものが「効用関数」であり、グラフで表したものが「効用曲線」です。これはたとえば、魚を10尾買って消費したら、100の満足感を得られたという形になります。
限界効用 marginal utility
新たに1単位買って、さらに増えた満足感(効用)を「限界効用」marginal utilityといいます。上の例でみると、10尾を消費した後で、さらに1尾を味わったら、どれだけ満足感が増えるかを表します。
仮定
「飽きることは無い」と仮定します。これは、消費すればするほど、効用は増えていくことです。ただし、この効用の増え方は、だんだんと少なくなっていきます(一般的なケース)。このことを、「限界効用逓減の法則」law of diminishing marginal utility(直訳:減っていく限界効用の法則)といいます。この様子を、グラフで表すとこうなります。
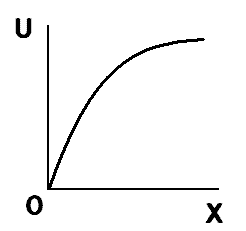
横軸のXは商品の消費量、縦軸のUは効用です。
ここで注意していただきたいのは、満腹になったからこのように感じるのではないということです(さきほど、「飽きることは無い」と仮定しました)。たくさん消費できれば、それだけ効用は増え続けます。でも、増え方が小さくなっていくということです。
ところで、この「限界効用逓減の法則」は、身近な感覚から導き出されたものといいました。
ということは他の例もあるということです。一応みていきましょう。
注意
バイオレンスな表現が続きます。
限界効用一定
うはは!!!

うはは!!!

うはは!!!

グラフで表すとこうなります。
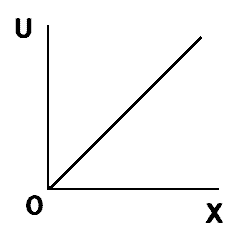
別のケースもあります。
限界効用逓増
これは、消費量が増えれば増えるほど追加的に感じる効用が高まっていくことを意味します。
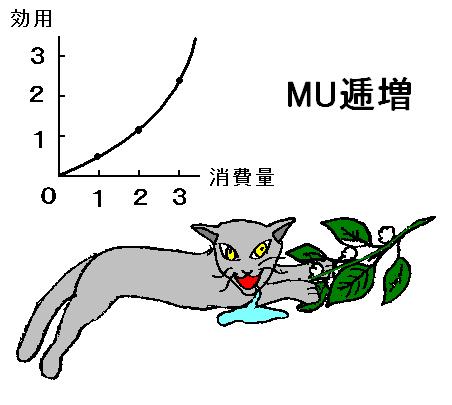
ご覧のように、かなりあぶない様子です。
経済学では、「限界効用逓減の法則」のケースを理解しておけばOKです。